Logaritma definīcija
Logaritma definīcija
Par skaitļa b logaritmu, ja bāze ir skaitlis a (a > 0 un a  1), sauc kāpinātāju, ar kuru kāpinot bāzi a, iegūst skaitli b.
Tātad, ja ac = b, tad logab = c, a > 0 un a 1
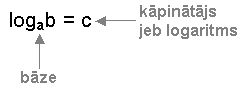
Aprēķināt logaritmu nozīmē noteikt kāpinātāju. Aprēķināt log28 nozīmē noteikt kāpinātāju, ar kuru kāpinot skaitli 2, iegūst 8. Tātad, log28 = 3, jo 23 =8
Piemēri
log327 = 3, jo 33 = 27
log0,2 = 1, jo 0,21 =
log4  = -3, jo (4)-3 =
Ja bāze ir skaitlis 10, tad logaritmu pieņemts saukt par decimāllogaritmu un pierakstīt šādi: log10100 = lg100.
Ja bāze ir iracionāls skaitlis e * e=2,718281828459*, tad logaritmu pieņemts saukt par naturāllogaritmu un pierakstīt šādi: loge6 = ln6.
No logaritma definīcijas izriet logaritmiskā pamatidentitāte alogab = b, kur logab ir kāpinātājs, ar kuru tiek kāpināts skaitlis a, lai iegūtu skaitli b.
|
|
