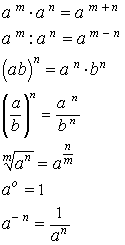Bieži eksponentnevienādības, izmantojot
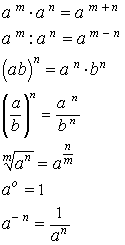
• Iznest pirms iekavām kopīgo reizinātāju;
• sadalīt reizinātājos;
• lietot substitūciju metodi.
ir iespējamas pārveidot formā af(x)< ag(x). Lai atrisinātu šādas nevienādības, izmanto eksponentfunkcijas monotonitātes īpašību.
Ja a > 1, tad eksponentfunkcija ir monotoni augoša un tāpēc,
ja af(x) < ag(x), tad f(x) < g(x).
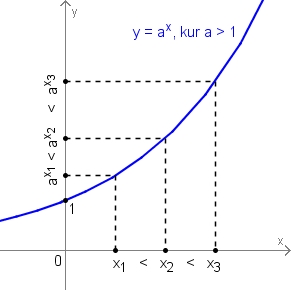
Ja 0 < a < 1, tad eksponentfunkcija ir monotoni dilstoša un tāpēc,
ja af(x) < ag(x), tad f(x) > g(x).
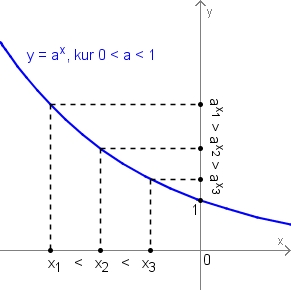
Ja a > 1, tad af(x) > ag(x) ↔ f(x) > g(x), af(x) < ag(x) ↔ f(x) < g(x)
Ja 0 < a < 1, tad af(x) > ag(x) ↔ f(x) < g(x), af(x) < ag(x) ↔ f(x) > g(x)
Piemēri.
1. Nevienādību 4x - 2 > 0,25, izmantojot pakāpju īpašības, var pārveidot par 4x -2 > 4-1

Tā kā bāze 4 > 1, tad x - 2 > -1 un x > 1
2. Nevienādību 0,5x + 4 ≥ 0,125x var pārveidot par0,5x+4 ≥ 0,53x
Tā kā bāze 0,5 < 1, tad x + 4 ≤ 3x un x ≥ 2