Izmantojot substitūcijas metodi, dažus logaritmiskos vienādojumus var pārveidot par algebriskiem vienādojumiem - kvadrātvienādojumiem, racionāliem daļveida vienādojumiem.
Piemērs
Logaritmisko vienādojumu log23 x - 6 log3 x + 5 = 0, izmantojot substitūciju log3 x = a, var pārveidot par vienādojumu a2 - 6a + 5 = 0, kura atrisinājumi ir a = 1 un a = 5.
Tātad log3 x = 1 un pēc logaritma definīcijas
Par skaitļa b logaritmu, ja bāze ir skaitlis a (a > 0 un a  1 ), sauc kāpinātāju, ar kuru kāpinot bāzi a iegūst skaitli b.
Ja ac = b, tad loga b = c, a > 0 un a 1 x = 31
x = 3
log3 x = 5
x = 35
x = 243
Abas vienādojuma saknes ietilpst definīcijas apgabalā x > 0.
Atbilde: x1 = 3; x2 = 243
Piemēri
Atrisināt vienādojumu 
Apzīmē lg x = a
Tad    4a(1 - a) = 1 4a - 4a2 = 1 4a2 - 4a + 1 =0 
Iegūto a vērtību ievieto vienādībā lg x = a, iegūst 
Pārbauda sakni:
- vienādība ir patiesa
Vienādojuma atrisinājums .
|
| 2011-05-23 22:09 Ieteikt draugiem TweetMe
|
|
Logaritmiskā funkcija ir monotona, tāpēc loga x1 = loga x2 tikai tad, ja x1 = x2. Ja logaritmisko vienādojumu, izmantojot logaritma īpašības, iespējams pārveidot formā loga f(x) = loga g(x), tad atrisinājumu iegūst, atrisinot vienādojumu f(x) = g(x). Šiem vienādojumiem jānosaka definīcijas apgabals: f(x) > 0 un g(x) > 0.
logaf(x) = logag(x)
Risinot sistēmu, vienu (jebkuru) no divām nevienādībām (f(x) > 0 un g(x) > 0) drīkst atmest, jo katra no tām izriet no sistēmas pirmā vienādojuma un otras nevienādības.
Piemērs
log5 2x = log5 (x2 - 3)
Vienādojuma atrisinājums ir x = 3.
Šāda veida vienādojumu var risināt arī citādi: atrisina vienādojumu f(x) = g(x) un tad pārbauda, kuras no iegūtajām saknēm ietilpst definīcijas apgabalā - tās tad arī ir logaritmiskā vienādojuma atrisinājumi.
Piemērs
log5 2x = log5 (x2 - 3)
2x = x2 - 3
x2 - 2x - 3 = 0
x1 = 3 x2 = -1
Pārbauda saknes:
Ja x = 3, tad 2 · 3 > 0; 6 > 0 - patiesa nevienādība;
ja x = -1, tad 2 · (-1) > 0; -2 > 0 - aplama nevienādība.
Vienādojuma atrisinājums ir x = 3.
|
| 2011-05-23 21:55 Ieteikt draugiem TweetMe
|
|
Logaritmiskā funkcija ir monotona, tāpēc loga x1 = loga x2 tikai tad, ja x1 = x2. Ja logaritmisko vienādojumu, izmantojot logaritma īpašības, iespējams pārveidot formā loga f(x) = loga g(x), tad atrisinājumu iegūst, atrisinot vienādojumu f(x) = g(x). Šiem vienādojumiem jānosaka definīcijas apgabals: f(x) > 0 un g(x) > 0.
logaf(x) = logag(x)
Risinot sistēmu, vienu (jebkuru) no divām nevienādībām (f(x) > 0 un g(x) > 0) drīkst atmest, jo katra no tām izriet no sistēmas pirmā vienādojuma un otras nevienādības.
Piemērs
log5 2x = log5 (x2 - 3)
Vienādojuma atrisinājums ir x = 3.
Šāda veida vienādojumu var risināt arī citādi: atrisina vienādojumu f(x) = g(x) un tad pārbauda, kuras no iegūtajām saknēm ietilpst definīcijas apgabalā - tās tad arī ir logaritmiskā vienādojuma atrisinājumi.
Piemērs
log5 2x = log5 (x2 - 3)
2x = x2 - 3
x2 - 2x - 3 = 0
x1 = 3 x2 = -1
Pārbauda saknes:
Ja x = 3, tad 2 · 3 > 0; 6 > 0 - patiesa nevienādība;
ja x = -1, tad 2 · (-1) > 0; -2 > 0 - aplama nevienādība.
Vienādojuma atrisinājums ir x = 3.
|
| 2011-05-23 21:55 Ieteikt draugiem TweetMe
|
|
Lai atrisinātu vienādojumu logaf(x) = b, izmanto logaritma definīciju.
Vienādojuma atrisinājums iegūstams, atrisinot vienādojumu f(x) = ab
logaf(x) = b
f(x) = ab
log3 x = 2
x = 32
x = 9 |
log7 (4x-5) = 1
4x-5 = 71
4x = 12
x = 3
|
|
| 2011-05-23 21:50 Ieteikt draugiem TweetMe
|
|
Par logaritmiskajiem vienādojumiem sauc vienādojumus, kuros nezināmais ietilpst logaritmiskās funkcijas bāzē vai argumentā.
Piemēram, logaritmiskie vienādojumi ir:
log2(x - 1) = 4,
log0,25 x - log0,25(2 + x) = 1
lg10x2 = lg90
Ja logaritmiskais vienādojums satur nezināmo bāzē, tad bāzei jābūt pozitīvai un tā nedrīkst būt vienāda ar 1. Tātad, ja logaritmiskais vienādojums satur logg(x)f(x), tad definīcijas apgabals ir sistēmas atrisinājums:
|
| 2011-05-23 21:41 Ieteikt draugiem TweetMe
|
|
Dažkārt logaritmisko izteiksmju pārveidojumos un aprēķinos ir lietderīgi pāriet uz citu bāzi, lai vienkāršotu veicamās darbības. To izdara, izmantojot bāzu pārejas formulu:
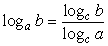
Piemērs
Aprēķināt log53 vērtību ar kalkulatoru. Ar kalkulatoru ir iespējams aprēķināt decimāllogaritma vērtības. Izmantojot bāzu pārejas formulu, izteiksmi log53 pārveido par decimāllogaritmu dalījumu un aprēķina decimāllogaritmu vērtības ar kalkulatoru:
|
| 2011-05-23 21:35 Ieteikt draugiem TweetMe
|
|
Izmantojot pakāpju īpašības, iespējams pamatot logaritmu īpašības, kuras izmanto, lai pārveidotu izteiksmes, kas satur logaritmus:
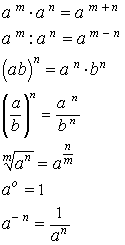
1. logc a + logc b = logc ab
2. logc a - logc b = logc 
3. logc ab = b · logc a
Piemērs
log627 - log63 + 2log62 =
= log6(27:3) +2log62 =
= log69 + log622 =
= log69 + log64 =
= log6(9 · 4) =
= log636 =
= 2
|
| 2011-05-23 21:28 Ieteikt draugiem TweetMe
|
|
Izmantojot pakāpju īpašības, iespējams pamatot logaritmu īpašības, kuras izmanto, lai pārveidotu izteiksmes, kas satur logaritmus:
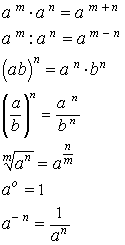
1. logc a + logc b = logc ab
2. logc a - logc b = logc
3. logc ab = b · logc a
Piemērs
log627 - log63 + 2log62 =
= log6(27:3) +2log62 =
= log69 + log622 =
= log69 + log64 =
= log6(9 · 4) =
= log636 =
= 2
|
| 2011-05-23 21:28 Ieteikt draugiem TweetMe
|
|
Logaritma definīcija
Par skaitļa b logaritmu, ja bāze ir skaitlis a (a > 0 un a 1), sauc kāpinātāju, ar kuru kāpinot bāzi a, iegūst skaitli b.
Tātad, ja ac = b, tad logab = c, a > 0 un a 1
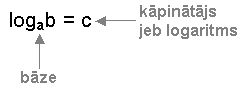
Aprēķināt logaritmu nozīmē noteikt kāpinātāju. Aprēķināt log28 nozīmē noteikt kāpinātāju, ar kuru kāpinot skaitli 2, iegūst 8. Tātad, log28 = 3, jo 23 =8
Piemēri
log327 = 3, jo 33 = 27
log0,2 = 1, jo 0,21 =
log4  = -3, jo (4)-3 =
Ja bāze ir skaitlis 10, tad logaritmu pieņemts saukt par decimāllogaritmu un pierakstīt šādi: log10100 = lg100.
Ja bāze ir iracionāls skaitlis e * e=2,718281828459*, tad logaritmu pieņemts saukt par naturāllogaritmu un pierakstīt šādi: loge6 = ln6.
No logaritma definīcijas izriet logaritmiskā pamatidentitāte alogab = b, kur logab ir kāpinātājs, ar kuru tiek kāpināts skaitlis a, lai iegūtu skaitli b.
|
| 2011-05-23 21:23 Ieteikt draugiem TweetMe
|
|
Līdzīgi eksponentvienādojumiem, arī eksponentnevienādības, izmantojot substitūcijas metodi, var pārveidot par algebriskām nevienādībām - kvadrātnevienādībām vai racionālām daļveida nevienādībām.
Piemērs.
72x - 4 · 7x - 21 < 0
Izmanto substitūciju 7x = a, kur a > 0 un 72x = a2.
Iegūst kvadrātnevienādību a2- 4a - 21 < 0, kuras atrisinājums ir tās a vērtības, kas pieder intervālam (-3;7). Taču tā kā a > 0, tad atbilstošās a vērtības pieder intervālam (0,7).
Ja a (0;7), tad 7x(0;7), jeb 0 < 7x<7. Tā kā 0 < 7x visām x vērtībām, jāatrisina vienīgi nevienādība 7x < 7. Tās atrisinājums ir x < 1 |
| 2011-05-23 21:10 Ieteikt draugiem TweetMe
|
|
|
|
